Question

Use the Rational Root Theorem to determine all POSSIBLE rational zeros. f(x)=2x^3-6x^2+9x-27

Answer 1

`\displaystyle{\text{possible rational roots} = \pm 1, \pm (1)/(2), \pm 3, \pm (3)/(2), \pm 9, \pm (9)/(2), \pm 27, \pm (27)/(2)}`

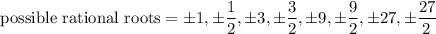
Explanation:

Rational Root theorem is when we divide the factors of last term by the factors of first term:

`\displaystyle{\text{possible rational roots} = \frac{\text{factors of the coefficient of last term (constant)}}{\text{factors of lead coefficient (coefficient of first term)}}}`

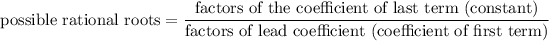
Our constant (last term) is -27. The factors of -27 can be ±1, ±3, ±9, ±27

Our lead coefficient is 2. The factors of 2 can be ±1 and ±2.

Hence:

`\displaystyle{\text{possible rational roots} = (\pm 1, \pm 3, \pm 9, \pm 27)/(\pm 1, \pm 2)}\\\\\displaystyle{\text{possible rational roots} = \pm 1, \pm (1)/(2), \pm 3, \pm (3)/(2), \pm 9, \pm (9)/(2), \pm 27, \pm (27)/(2)}`

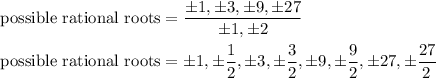
All of these are possible roots, meaning that not all of them are real roots of the equation, just a possibility.