Question

Please please help

Engineers have determined that the strengths of a rectangular beam varies as
the product of the width w and the square of the depth d of the beam, that is,
S = kwd2 for some constant k > 0.
a A particular cylindrical log has a diameter of 48 cm. Use Pythagoras' theorem
to show that s = kw (2304 - w²).
b Hence find the dimensions of the strongest rectangular beam that can be cut from
the log.

Answer 1

The dimensions of the strongest rectangular beam that can be cut from the log are:

• depth d = 16√6 cm
• width w = 16√3 cm

Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

Part (a)

From observation of the given diagram, the diameter of the circle is the hypotenuse of a right triangle (with legs w and d). Given that the diameter is 48 cm, substitute the values into Pythagoras' Theorem and rearrange to create an expression for d²:

`\begin{aligned}w^2+d^2&=48^2\\w^2+d^2&=2304\\d^2&=2304-w^2\end{aligned}`

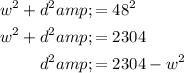
Substitute the found expression for d² into the given strength equation:

`\begin{aligned}s&=kwd^2\\s&=kw(2304-w^2)\end{aligned}`

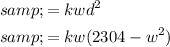
Hence showing that s = kw (2304 - w²).

Part (b)

To find the value of w that will maximise the strength of the rectangular beam, first differentiate the equation for s in terms of w:

`\begin{aligned}s&=kw(2304-w^2)\\s&=2304kw-kw^3\\\implies \frac{\text{d}s}{\text{d}w}&=2304k-3kw^2\\&=3k(768-w^2)\end{aligned}`

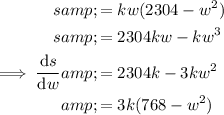
Set the differentiated equation to zero and solve for w:

`\begin{aligned}3k(768-w^2)&=0\\ 768-w^2&=0\\w^2&=768\\w&=√(768)\\w&=√(256 \cdot 3)\\w&=√(256)√(3)\\w&=16√(3)\\\end{aligned}`

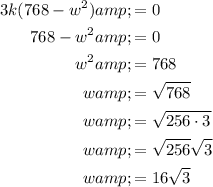
Substitute the value of w that maximises the strength of the beam, together with the given hypotenuse of 48 cm, into Pythagoras' Theorem and solve for d:

`\begin{aligned}w^2+d^2&=48^2\\768+d^2&=2304\\d^2&=2304-768\\d^2&=1536\\d&=√(1536)\\d&=√(256 \cdot 6)\\d&=√(256)√(6)\\d&=16√(6)\end{aligned}`

Therefore, the dimensions of the strongest rectangular beam that can be cut from the log are:

• depth d = 16√6 cm
• width w = 16√3 cm