Question

A car rental agency has 20 cars. Of those cars, 4 are

luxury sedans and all the other cars are midsize sedans.
Each luxury sedan rents at a daily rate 50% greater
than the daily rate for the midsize sedans. If the luxury
sedans rent for $45 per day, what is the average daily
rental fee, to the nearest dollar, of all 20 cars at this
agency?
A. $27
B. $33
C. $38
D. $42
E. $56

Answer 1

`\Huge \boxed{\textbf{B. \$33}}`

Explanation:

To solve this problem, we first need to find the daily rental rate for the midsize sedans. Since the luxury sedans rent for $45 per day and their daily rate is 50% greater than the midsize sedans, we can set up the following equation:

`\Large \boxed{\texttt{45 = 1.5 $*$ Midsize daily rate}}`

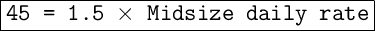
Now, we can solve for the midsize daily rate:

• 
  `\texttt{Midsize daily rate} = \tt{(45)/(1.5)}`

• 
  `\texttt{Midsize daily rate} = \tt{30}`

So, the midsize sedans rent for $30 per day. There are 16 midsize sedans (20 total cars - 4 luxury sedans) and 4 luxury sedans. To find the average daily rental fee for all 20 cars, we can use the following formula:

`\Large\boxed{\texttt{Average daily rental fee} = \frac{\texttt{Total rental fees}}{\texttt{Total number of cars}}}`

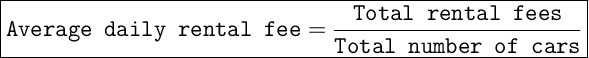
The total rental fees can be calculated as follows:

• 
  `\texttt{Total rental fees} = \tt{(16 * 30) + (4 * 45) }\\`

• 
  `\texttt{Total rental fees} = \tt{480 + 180}`

• 
  `\texttt{Total rental fees} = \tt{660}`

Now, we can find the average daily rental fee:

• 
  `\texttt{Average daily rental fee} = \tt{(660)/(20)} \\`

• 
  `\texttt{Average daily rental fee} = \tt{33}`

So, the average daily rental fee for all 20 cars at this agency is $33, which corresponds to option B.

#BTH1

________________________________________________________