1 Answer

Ask a Question

TimDog · Answer 1 · 2024-04-08T13:16:37+0000

Answer:

Maximum value: 9, located at point (-3, 9).

Minimum value: -5/3, located at point (1, -5/3).

Explanation:

1. Write the expression.

y=(1)/(3)x^(3) +x^(2) -3x

2. Recall and take the derivative by applying the differentiation rules for power.

Check attached images 1 and 2.

$(d)/(dx) =y'\\ \\y'=(3*(1)/(3))x^(3-1) +2*x^(2-1) -(1*3)x^(1-1) \\ \\y'=x^(2) +2x-3$

3. Find the roots of the derivative.

Use the quadratic formula.

Check attached image 3.

a = 1

b = 2

c = -3

$x_(1) =\frac{-(2)+\sqrt{(2)^(2)-4(1)(-3) } }{2(1)} =1\\ \\x_(2) =\frac{-(2)-\sqrt{(2)^(2)-4(1)(-3) } }{2(1)} =-3$

Quick analysis. This results tell us that the minimun and maximum points different that infinity of the original function (
y=(1)/(3)x^(3) +x^(2) -3x ) are located in points x = 1 and x = -3. Now, we need to discover who's the maximum point and who's the minimum. For this, evaluate both point in the original function.

4. Evaluate the points in the original equation.

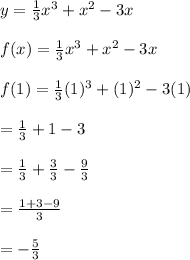
$y=(1)/(3)x^(3) +x^(2) -3x\\ \\f(x)=(1)/(3)x^(3) +x^(2) -3x\\ \\f(1)=(1)/(3)(1)^(3) +(1)^(2) -3(1)\\\\ =(1)/(3)+1-3 \\\\ =(1)/(3) +(3)/(3)-(9)/(3) \\ \\=(1+3-9)/(3) \\ \\=-(5)/(3)$

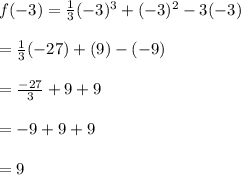
$f(-3)=(1)/(3)(-3)^(3) +(-3)^(2) -3(-3)\\ \\=(1)/(3)(-27) +(9)-(-9)\\ \\=(-27)/(3) +9+9\\ \\=-9+9+9\\ \\=9$

5. Conclude.

Maximum value: 9, located at point (-3, 9).

Minimum value: -5/3, located at point (1, -5/3).

Check out the graph (attached image 4) to better understand the method used for this solution.

Note. See that the "x" coordinates where the function has maximum and minimum points are the exact same "x" coordinates where the derivative touches the "y" axis, that's why we calculated the roots of the derivative and then evaluated in the original function.