Question

Explain the answer step by step please​

Answer 1

The answer is D.

The portion of the statement
`{x\to 0}` says we're looking at the graph as the x-values get closer to 0. So we're looking at x-values like 0.1, 0.01, 0.001, 0.0001, etc and -0.1, -0.01, -0.001, -0.0001, etc.

The
`\lim\limits_(x\to 0)f(x)`
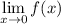
`\lim\limits_(x\to 0)f(x) = 1` as a whole is asking "are the y-values on the graph headed towards a specific y-value as x-values get closer to 0?"

As you move towards x = 0 from either side, the y-values get closer to y=1.

So
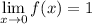`\lim\limits_(x\to 0)f(x)=1`.