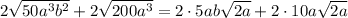Question

The dimensions of a rectangle are √50a^3b^2 and √200a^3. What is the students error?

Answer 1

D. The student incorrectly simplified 10ab sqrt2a+ 20a sqrt2a

Explanation:

Just did it.

Answer 2

The student incorrectly simplified
`30ab√(2a)+20a√(2a)` .

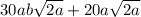Thus, option D is correct.

Explanation:

The formula to determine the Perimeter of a rectangle of width w and length l is expressed as:

`P = 2l + 2w`

In other words, the perimeter can be determined by multiplying the length and width by 2 and adding the result.

In our case, the dimensions of a rectangle are
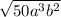`√(50a^3b^2)` and
`√(200a^3)\:\:`.

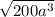Here is the student's solution:

`2√(50a^3b^2)+2√(200a^3)=2\cdot 5ab√(2a)+2\cdot 10a√(2a)`

`=10ab√(2a)+20a√(2a)`

`=30ab√(2a)`

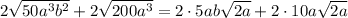
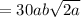
The student made an error in calculating
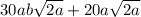`30ab√(2a)+20a√(2a)` , because
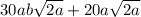`30ab√(2a)+20a√(2a)` are not like terms.

Hence,
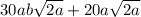`30ab√(2a)+20a√(2a)` can not be simplified to
`30ab√(2a)`

Therefore, the student incorrectly simplified
`30ab√(2a)+20a√(2a)` .

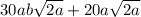Thus, option D is correct.

Here is the correct Solution:

`2√(50a^3b^2)+2√(200a^3)=2\cdot 5ab√(2a)+2\cdot 10a√(2a)`

`=10ab√(2a)+20a√(2a)`