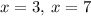Question

(x-2)^2-6(x-2)+5=0
Find a Value of X

Answer 1

The values of x are:

`x=3,\:x=7`

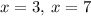
Explanation:

Given the expression

`(x-2)^2-6(x-2)+5=0`

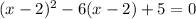
Expand (x - 2)² = x² -4x + 4

`x^2-4x+4-6\left(x-2\right)+5=0`

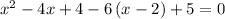
Expand: -6(x - 2) = -6x + 12

`x^2-4x+4-6x+12+5=0`

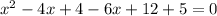
simplifying

`x^2-10x+21=0`

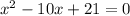
Factor x² -10x + 21: (x - 3) (x - 7)

`\left(x-3\right)\left(x-7\right)=0`

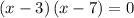
Using the zero factor principle

if ab=0, then a=0 or b=0 (or both a=0 and b=0)

`x-3=0\quad \mathrm{or}\quad \:x-7=0`

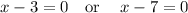
solving x - 3 = 0

x - 3 = 0

Adding 3 to both sides

`x-3+3=0+3`

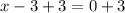
simplify

x = 3

solving x - 7 = 0

x - 7 = 0

Adding 7 to both sides

`x-7+7=0+7`

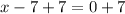
Simplify

x = 7

Therefore, the values of x are:

`x=3,\:x=7`