Question

consider the region bounded above by g(x)=−9x−9 and below by f(x)=x2−9x−18. find the area, in square units, between the two functions over the interval [−3,3].

Answer 1

The total area of the regions between the curves is 42 square units

Calculating the total area of the regions between the curves

From the question, we have the following parameters that can be used in our computation:

g(x) = -9x - 9 and f(x) = x² - 9x - 19

Also, we have the interval

[-3, 3]

So, the area of the regions between the curves is

`\text{Area} = \int\limits^a_b {[g(x) - f(x)]} \, dx`

This gives

`\text{Area} = \int\limits^3_(-3) {[-9x - 9 - x\² + 9x + 19]} \, dx`

`\text{Area} = \int\limits^3_(-3) {[- x\² + 10]} \, dx`

Integrate

`\text{Area} = [- (x^3)/(3) + 10x]|\limits^3_(-3)`

Expand

`\text{Area} = [- (3^3)/(3) + 10 * 3] - [- ((-3)^3)/(3) + 10 * -3]`

Evaluate

`\text{Area} = 21 + 21`

`\text{Area} = 42`

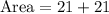
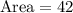
Hence, the total area of the regions between the curves is 42 square units