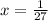Question

Condense the equation
2log9= log3 - logx

Answer 1

`x=(1)/(27)`

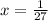
Explanation:

Solve for x.

We need to use the quotient property of logarithms.

Quotient Property of Logarithms:
`\log _(b) (x)-\log _(b) (y)=\log _(b) ((x)/(y) )`

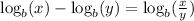
Apply the property to our equation.

`\log((3)/(x))=2\log(9)`

Simplify the right side by moving the 2 inside the logarithm.

`\log((3)/(x))=\log(9^2)`

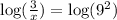
For the equation to be equal, the argument of the logarithms on both sides of the equation must be equal.

`(3)/(x)=9^2`

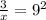
Evaluate
`9^2`.

`(3)/(x)=81`

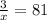
Multiply both sides of the equation by x.

`(3)/(x)x=81x`

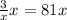
Cancel the common factor of x on the left side.

`3=81x`

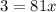
Divide both sides by 81.

`(3)/(81) =(81x)/(81)`

`(3)/(81) =x`

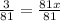
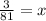
Simplify the fraction.

`x=(1)/(27)`