Answer:

The solution line graph is also attached.
Explanation:
Given
The inequality is given by
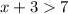
To determine
What is the solution to the inequality?
Solving the given inequality
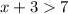
Subtract 3 from both sides
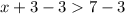
Simplify
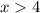
Thus,

The solution line graph is also attached.