Find the standard form of the equation for the conic section represented by x^2 + 10x + 6y = 47.

Question

asked Mar 21, 2022 72.8k views

1 Answer

Heather McVay · Answer 1 · 2022-03-26T00:22:48+0000

Answer:

The standard form of the equation for the conic section represented by
$x^2\:+\:10x\:+\:6y\:=\:47$ is:

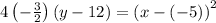
$4\left(-(3)/(2)\right)\left(y-12\right)=\left(x-\left(-5\right)\right)^2$

Explanation:

We know that:

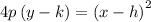$4p\left(y-k\right)=\left(x-h\right)^2$ is the standard equation for an up-down facing Parabola with vertex at (h, k), and focal length |p|.

Given the equation

$x^2\:+\:10x\:+\:6y\:=\:47$

Rewriting the equation in the standard form

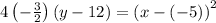
$4\left(-(3)/(2)\right)\left(y-12\right)=\left(x-\left(-5\right)\right)^2$

Thus,

The vertex (h, k) = (-5, 12)

Please also check the attached graph.

Therefore, the standard form of the equation for the conic section represented by
$x^2\:+\:10x\:+\:6y\:=\:47$ is:

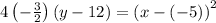
$4\left(-(3)/(2)\right)\left(y-12\right)=\left(x-\left(-5\right)\right)^2$

where

vertex (h, k) = (-5, 12)