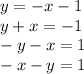Question

Need help quick

Find the equation of a line perpendicular to -x=3-y that passes through the point (8,-9).

A. -x-y=1
B. Y=x-1
C. Y=-x+3
D. -x+y=-17

Answer 1

A. -x-y=1

Explanation:

The general form of a linear line is y = mx + b

By letting m2 represent the slope of the unknown line and m1 the slope of the line we're given, we can find m2 using the formula:

`m_(2)=(-1)/(m_(1) )`

Currently, the line -x=3-y is in standard form (i.e., Ax + By = C) and we must convert it so slope-intercept form to find the slope (i.e., y = mx + b):

`-x=3-y\\-x-3=-y\\x+3=y`

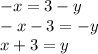
Thus, the slope is 1. This slope is m1 and we can use it to find m2:

`m_(2)=(-1)/(1) \\m_(2)=-1`

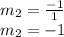
We can now find the y-intercept of the second line by plugging in the slope and the point we're given:

`-9=-1(8)+b\\-9=-8+b\\-1=b`

Thus, the equation of the line in slope-intercept form is y = -x - 1.

We can convert it standard form by moving x to the left side and dividing by -1:

`y=-x-1\\y+x=-1\\-y-x=1\\-x-y=1`