Question

NO LINKS!!

Please help me with #6 and 8

Answer 1

6) x = 6

8) GH = 47

Explanation:

SAS Similarity Theorem

If two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.

Question 6

If two triangles are similar, their corresponding sides are proportional.

According to the given diagram, the sides of the larger triangle are twice the length of the sides of the smaller similar triangle. Therefore, the ratio of sides of the smaller to larger triangle is 1 : 2.

Set up an equivalent ratio and solve for x:

`\implies 1:2=(6x+7):(19x-28)`

`\implies (1)/(2)=(6x+7)/(19x-28)`

`\implies 19x-28=2(6x+7)`

`\implies 19x-28=12x+14`

`\implies 7x=42`

`\implies x=6`

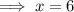
Question 8

If two triangles are similar, their corresponding sides are proportional.

According to the given diagram, the sides of the larger triangle are twice the length of the sides of the smaller similar triangle. Therefore, the ratio of sides of the smaller to larger triangle is 1 : 2.

Set up an equivalent ratio and solve for x:

`\implies 1:2=GH:DF`

`\implies 1:2=(3x-4):(9x-59)`

`\implies (1)/(2)=(3x-4)/(9x-59)`

`\implies 9x-59=2(3x-4)`

`\implies 9x-59=6x-8`

`\implies3x=51`

`\implies x=17`

To find the length of GH, substitute the found value of x into the expression for GH:

`\implies GH=3(17)-4`

`\implies GH=51-4`

`\implies GH=47`