Question

SOLVE THE SYSTEM ALGEBRAICALLY

Answer 1

Answer: (4,3) and (-1,8)

Explanation:

Before I solve the system, I am going to rewrite it to make it easier for me to understand it.

`y=x^2-4x+3\\y=-x+7`

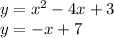
Notice that f(x) and g(x) have been changed into y. The reason is because f(x) and g(x) are the same and stand for y, but we only use f and g to distinguish between the 2 equations. We can use equal values to solve.

`x^2-4x+3=-x+7` [add both sides by x]

`x^2-3x+3=7` [subtract both sides by 7]

`x^2-3x-4=0` [factor]

`(x-4)(x+1)=0`

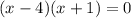
Notice that x-4=0 and x+1=0. This means the solutions are x=4 and x=-1.

To find the actual full solution, we have to plug those points back into the original equations.

`-(4)+7=-4+7=3\\-(-1)+7=1+7=8`

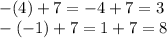
Therefore, the solutions to this system are (4,3) and (-1,8).