To find:-
Answer:-
We are here given that, an arc subtends an angle of 11π/6 radians on the centre of a circle whose radius is 18cm . We that the if r is the radius of a circle and
 is the angle substended by an arc at the centre then, the length of the arc is given by,
is the angle substended by an arc at the centre then, the length of the arc is given by,
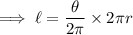
where ,
 is the angle in radians .
is the angle in radians .
 is the arc length.
is the arc length.
Now on substituting the respective values, we have;
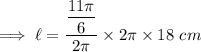
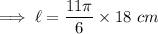
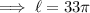

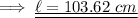
Hence the length of the arc is 103.62 cm .
and we are done!