Answer:
The length of the roof of the house, x, is 50 ft.
Explanation:
From observation of the given diagram, we can see that the length of the roof "x" is the hypotenuse of a right triangle. Therefore, we can use Pythagoras Theorem to calculate the value of x.

From observation of the given diagram, the lengths of the legs of the right triangle are 30 ft and 40ft, and the hypotenuse is x ft:
- a = 30 ft
- b = 40 ft
- c = x ft
Substitute the values of a, b and c into Pythagoras Theorem formula and solve for x:
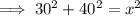

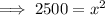
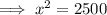

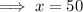
Therefore, the length of the roof of the house is 50 ft.