Question

Let R be the region bounded by the following curves Find the volume of the solid generated when R is revolved about the y-axis y=6x y=24 y=X,y= 6x,y= 24 Set up the integral that gives the volume of the solid. dy (Type exact answers_ The volume of the solid is (Type an exact answer) cubic units'

Answer 1

`V=4480\pi \text{ units}^3`

Explanation:

Rewrite the region in terms of x

`\displaystyle x=(y)/(6),\,x=y,\,y=24`

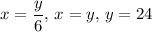
Identify inner and outer radii

The inner radius is
`\displaystyle r=(y)/(6)` and the outer radius is
`R=y` because as
`y` goes from 0 to 24,
`x` goes from
`\displaystyle x=(y)/(6)` to
`x=y` in that direction.

Perform Washer Method

`\displaystyle V=\pi\int\limits^b_a {(R^2-r^2)} \, dy\\ \\V=\pi\int\limits^(24)_0 {\biggr(y^2-\biggr((y)/(6)\biggr)^2\biggr)} \, dy\\\\V=\pi\int\limits^(24)_0 {\biggr(y^2-(y^2)/(36)\biggr)\biggr)} \, dy\\\\V=\pi\biggr((y^3)/(3)-(y^3)/(108)\biggr)\biggr|_0^(24)\\\\V=\pi\biggr((24^3)/(3)-(24^3)/(108)\biggr)\\ \\V=4480\pi \text{ units}^3`

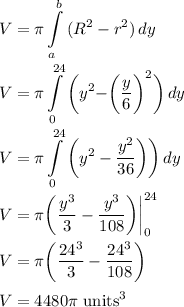
I've attached a visual to help better understand this problem!