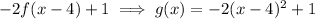Answer:
1. Translation of 4 units right.
2. Vertical stretch by a factor of 2:
3. Reflection in the x-axis:
4. Translation of 1 unit up.
Explanation:
Transformations
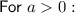

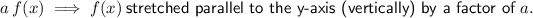

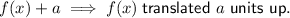
Given function:
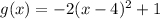
The parent function of the given function is:
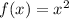
When determining the sequence of transformations when the function contains more than one transformation, follow the order of operations (PEMDAS).
1. Translation of 4 units right.
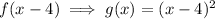
2. Vertical stretch by a factor of 2:
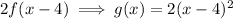
3. Reflection in the x-axis:
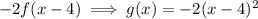
4. Translation of 1 unit up.