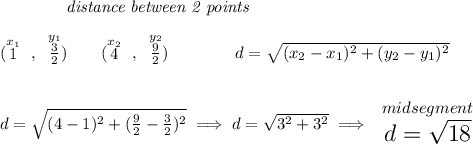Question

The length of the mid segment is:

Answer 1

Check the picture below.

so from the picture below we can say that parallel sides or bases of the trapezoid are AB and DC, that means our midsegment is found halfway of BC and halfway of AD, let's get the midpoints for those and then get their length.

`~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ A(\stackrel{x_1}{0}~,~\stackrel{y_1}{3})\qquad D(\stackrel{x_2}{2}~,~\stackrel{y_2}{0}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left(\cfrac{ 2 +0}{2}~~~ ,~~~ \cfrac{ 0 +3}{2} \right) \implies \left(\cfrac{ 2 }{2}~~~ ,~~~ \cfrac{ 3 }{2} \right)\implies (1~~,~~(3)/(2)) \\\\[-0.35em] ~\dotfill`

`~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ B(\stackrel{x_1}{2}~,~\stackrel{y_1}{5})\qquad C(\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left(\cfrac{ 6 +2}{2}~~~ ,~~~ \cfrac{ 4 +5}{2} \right) \implies \left(\cfrac{ 8 }{2}~~~ ,~~~ \cfrac{ 9 }{2} \right)\implies (4~~,~~(9)/(2))`

let's get their distance

`~~~~~~~~~~~~\textit{distance between 2 points} \\\\ (\stackrel{x_1}{1}~,~\stackrel{y_1}{(3)/(2)})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{(9)/(2)})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ d=\sqrt{(4-1)^2 + ((9)/(2)-(3)/(2))^2}\implies d=√(3^2 + 3^2)\implies {\Large \begin{array}{llll} \stackrel{midsegment}{ d=√(18)} \end{array}}`