Question

You deposit $120 in an investment account that earns 6.4% annual interest compounded quarterly write a function that represents the balance y (in dollars) of the investment account after t years y= ? What is the balance of the account after 6 years

Answer 1

Answer:1200

Explanation:

Answer 2

`\textsf{Function:} \quad y=120\left(1.016\right)^(4t)`

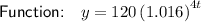
The balance of the account after 6 years is $175.64 (nearest cent).

Explanation:

To write a function that represents the balance y (in dollars) of the investment account after t years, substitute the given values into the compound interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Given values:

• A = y
• P = $120
• r = 6.4% = 0.064
• n = 4 (quarterly)
• t = t years

Substitute these values into the formula:

`\implies y=120\left(1+(0.064)/(4)\right)^(4t)`

`\implies y=120\left(1+0.016\right)^(4t)`

`\implies y=120\left(1.016\right)^(4t)`

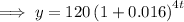
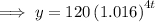
To calculate the balance of the account after 6 years, substitute t = 6 into the function:

`\implies y=120\left(1.016\right)^(4 \cdot 6)`

`\implies y=120\left(1.016\right)^(24)`

`\implies y=120\left(1.46368961...\right)^(24)`

`\implies y=175.642753...`

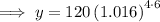
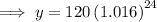
Therefore, the balance of the account after 6 years is $175.64 (nearest cent).