Question

An automobile traveling initially at a speed of 60 m/s is accelerated uniformly to a speed of 85 m/s in 12 s. How far does the automobile travel during the 12 s interval?

Answer 1

870 m

Step-by-step explanation:

d = Vit + 1/2at²

a = ΔV/Δt = (85 m/s - 60 m/s) / (12 s) = (25 m/s) / 12 s = 2.08 m/s²

d = (60 m/s)(12 s) + 1/2 (2.08 m/s²)(12 s)² = 870 m

Answer 2

The automobile traveled 870 meters during the 12 second interval.

Step-by-step explanation:

We can use this kinematics equation to evaluate how far the automobile traveled.

`\overline v=(\Delta x)/(\Delta t)`

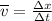
Note

`\overline v` is the average velocity

`\Delta x` is the change in position (displacement)

`\Delta t` is the change in time (time interval)

The formula for average velocity is

`\overline v=(V_f-V_o)/(2)`

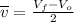
We are given

`V_f=85\\V_o=60\\\Delta t=12`

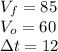
First lets evaluate the average velocity.

`\overline v=(85-60)/(2)`

`\overline v=72.5`

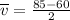
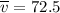
Rearranging our kinematics equation to isolate
`\Delta x` we get

`\Delta x=\overline v \Delta t`

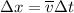
Now lets evaluate
`\Delta x`.

`\Delta x=72.5*12\\\Delta x=870`

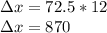
There are many different ways you can solve this; I could have used a different equation.