Answer:
Option B
Domain: all real numbers
Range
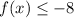
Explanation:
Given function is:
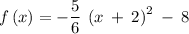
The domain is the set of all x values that result in a real and defined value for f(x).
The function has no undefined points and x is free to range from -∞ to +∞
So the domain is -∞ < x <∞ which is
All real numbers
The range is the set of all possible values for f(x) given a specific domain. In order to determine the range without too much hard work, let's first examine the function f(x)
The above function is the equation for a parabola.
Some things to note about a parabola equation:
- The vertex form equation of a parabola is:
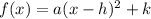
where the vertex is the point (h, k). So the x-value of the vertex = h and corresponding y-value is - A vertex is the maximum or minimum point in the parabola
- If the coefficient a > 0 then the parabola opens upward and the vertex i(h, k) s a minimum
- If the coefficient, a < 0 the parabola opens downward and the vertex (h, k) is a maximum
Let us compare the general vertex form equation of the parabola with the specific f(x) equation given
General Equation:
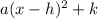
This example:
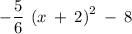
Comparing the similarity between the two equations we easily see that

This means the parabola opens downward and (h, k) represents a max point in the parabola

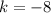
So the vertex is at (-2, -8)
Since -8 is the maximum value for f(x), and the parabola extends to infinity on both sides, the range is :

The attached graph may help you understand better