Question

What is the solution set for the compound inequality? 3x - 2 > - 11 and - 2x + 1 < - 3

Answer 1

D. x

Explanation:

Separately solve inequalities:

`\displaystyle{3x-2 > -11 \ \: \text{and} \ \: -2x+1 < -3}`

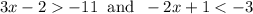
For left inequality, add 2 both sides. For right inequality, subtract 1 both sides:

`\displaystyle{3x-2 +2 > -11+2 \ \: \text{and} \ \: -2x+1-1 < -3-1}\\\\\displaystyle{3x > -9 \ \: \text{and} \ \: -2x < -4}`

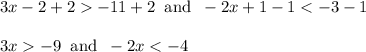
For left inequality, divide both sides by 3. For right inequality, divide both sides by -2 and also switch from < to > since the coefficient of x is negative:

`\displaystyle{(3x)/(3) > (-9)/(3) \ \: \text{and} \ \: (-2x)/(-2) > (-4)/(-2)}\\\\\displaystyle{x > -3 \ \: \text{and} \ \: x > 2}`

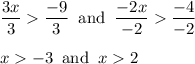
Since both are in form of x > a and x > b, consider for highest value (since putting value below than 2 would make the other inequality false but if we put value higher than 2 then it'd make both inequalities true) which is x > 2.