Question

Solve for x using logarithms.


`3^(2-3x) = 4^(2x+1)`

Answer 1

`\large\boxed{\sf 0.133 }`

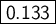
Explanation:

The given equation to us is ,

`\longrightarrow 3^(2-3x)= 4^(2x+1) \\`

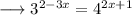
Take log to base 10 on both sides,

`\longrightarrow \log_(10) 3^(2-3x)= \log_(10) 4^(2x+1) \\`

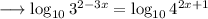
Now recall that,
`\log a^m = m\ log \ a`

`\longrightarrow (2-3x) \log_(10) 3 = (2x+1)(\log_(10) 4)\\`

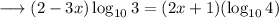
We can write it as ,

`\longrightarrow (2-3x) \log_(10)3=(2x+1)\log_(10)2^2 \\`

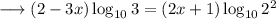
Again using the property mentioned above,

`\longrightarrow (2-3x)\log_(10)3 = 2(2x+1)\log_(10) 2 \\`

`\longrightarrow (2-3x)\log_(10)3 = (4x+2)\log_(10) 2 \\`

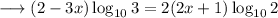
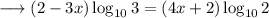
Now we know that ,

• log 3 = 0.477
• log 2 = 0.301

On substituting the values, we have ,

`\longrightarrow (2-3x)0.477 = (4x+2)0.301 \\`

simplify by opening the brackets,

`\longrightarrow 0.954 - 1.431x = 1.204x + 0.602 \\`

`\longrightarrow 1.204x + 1.431x = 0.954 - 0.602 \\`

`\longrightarrow 2.635x = 0.352 \\`

`\longrightarrow x =(0.352)/(2.635) \\`

`\longrightarrow \underline{\underline{ x = 0.133 }} \\`

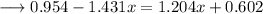
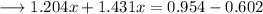
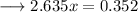
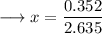
and we are done!