Question

Olivia flips a coin and rolls a number cube with sides labeled 1, 2, 3, 4, 5, and 6. After 90 trials of the experiment, the relative frequency of flipping heads and rolling a number less than 3 is 2/15 . What is the difference between the number of expected outcomes and the number of actual outcomes?

Answer 1

3

Explanation:

Experimental probability is based on the actual outcomes of an experiment (gathered by experimenting repeatedly).

Theoretical probability is based on the possible outcomes (expected outcomes).

Probability formula

`\boxed{\sf Probability\:of\:an\:event\:occurring = (Number\:of\:ways\:it\:can\:occur)/(Total\:number\:of\:possible\:outcomes)}`

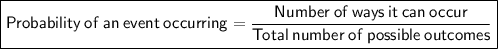
Theoretical probability of flipping a head

A coin has two sides: one side is a "head", the other side is a "tail".

The number of ways flipping a head can occur is 1.

The total number of possible outcomes is 2.

Therefore, the theoretical probability of flipping a head is 1/2.

Theoretical probability of rolling a number less than 3

The cube has six sides labelled 1, 2, 3, 4, 5 and 6.

The number of ways that rolling less than 3 can occur is 2 (rolling 1 or 2).

The total number of possible outcomes is 6.

Therefore, the theoretical probability of rolling a number less than 3 is 2/6 = 1/3.

Therefore, the theoretical probability of flipping a head and rolling a number less than 3 is:

`\sf P(head)\; and\; P(X < 3)=(1)/(2) * (1)/(3)=(1)/(6)`

To calculate the number of actual outcomes and expected outcomes after 90 trials, multiply the number of trials by the probability for each outcome:

`\textsf{Number of actual outcomes}=90 * (2)/(15)=12`

`\textsf{Number of expected outcomes}=90 * (1)/(6)=15`

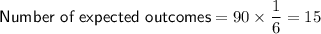
Therefore, the difference between the number of expected outcomes and the number of actual outcomes is:

`\implies 15-12=3`

Note: If Olivia continued to flip the coin and roll the number cube, as the number of trials increased, we would expect the experimental probability of 2/15 to get nearer to the theoretical probability of 1/6 and so the difference between the number of actual and expected outcomes would become smaller.