Question

A plane is on its approach to land on the runway. The jet’s height above the ground is given in feet as a function of the time in seconds. The following table tracks the plane as it lands:

t (in seconds)
h (in feet)
0
4000
5
3500
10
3000
15
2500
20
2000
25
1500

Is this function linear? If it is, what is the slope? Use the formula m = StartFraction delta h Over delta t EndFraction.
a.
No, this is not a linear function.
b.
Yes, this function is linear; the slope is 500 feet/second.
c.
Yes, this function is linear; the slope is 100 feet/second.
d.
Yes, this function is linear; the slope is -100 feet/second.

Answer 1

d. Yes, this function is linear; the slope is -100 feet/second.

Explanation:

Find the difference in height at two different time periods.

If

Δh = difference in height values

Δt = difference in seconds

then

`\mathrm{slope = (\Delta h)/(\Delta y)}`

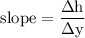
Take the difference in heights at t = 0 and t = 5

The height drops from 4000 to 3500 feet so Δh = 3500 - 400 = -500

Δt = 5- 0 = 5 seconds

slope = -500/5 = -100

If you compute the slope between any pair of heights and time difference you will get the same value

So slope is constant indicating a linear function