Question

Due to the installation of a muffler, the noise level of an engine decreased from 88 to 72 decibels. Find the percent decrease in the intensity of the noise as a result of the installation of the muffler given the following information:

The number of decibels
`\beta` of a sound with an intensity of
`I` watts per square meter is given by
`\beta = 10\log\left((I)/(I_0)\right)`.



`I_0` is an intensity of
`10^(-12)` watts per square meter, corresponding roughly to the faintest sound that can be heard by the human ear.

Answer 1

97.5% decrease

Explanation:

You want the percentage change in noise intensity when it is reduced from 88 to 72 dB.

Intensity ratio

The intensity can be found by solving the given equation for I:

`\beta_1=10\log\left((I_1)/(I_0)\right)\\\\10^(\beta_1/10)=(I_1)/(I_0)\\\\I_1=I_0\cdot10^(\beta_1/10)`

Similarly, the reduced intensity is ...

`I_2=I_0\cdot10^(\beta_2/10)`

Percent change

The percentage change is found from ...

percentage change = (I₂/I₁ -1) × 100%

Using the above expressions for I₁ and I₂, this becomes ...

`\text{\% change}=\left((I_0\cdot10^(\beta_2/10))/(I_0\cdot10^(\beta_1/10))-1\right)*100\%\\\\=(10^((\beta_2-\beta_1)/10)-1)*100\%=(10^((72-88)/10)-1)*100\%\\\\=(10^(-1.6)-1)*100\% \approx -0.975*100\% =\boxed{ -97.5\%}`

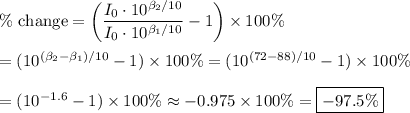
The noise intensity decreased by about 97.5%.

__

Additional comment

It can be useful to remember that log(2) ≈ 0.30103. That is, a reduction of 3 dB is a reduction by a factor of 2. Hence 16 db is a factor of about 40.

Answer 2

97.49% (2 d.p.)

Explanation:

Given equation:

`\beta=10 \log\left((I)/(I_0)\right)`

Divide both sides by 10:

`\implies (\beta)/(10)= \log\left((I)/(I_0)\right)`

Switch sides:

`\implies \log\left((I)/(I_0)\right)=(\beta)/(10)`

`\textsf{Apply log law}: \quad \log_ab=c \iff a^c=b`

`\implies 10^{(\beta)/(10)}=(I)/(I_0)`

Multiply both sides by I₀:

`\implies I=I_010^{(\beta)/(10)}\\`

Substitute the given value of I₀:

`\implies I=10^(-12) \cdot 10^{(\beta)/(10)}\\`

`\textsf{Apply exponent rule} \quad a^b \cdot a^c=a^(b+c):`

`\implies I=10^{\left((\beta)/(10)-12\right)}\\`

Therefore, the value of I when β = 88 dB is:

`\implies I=10^{\left((88)/(10)-12\right)}\\`

`\implies I=10^(-3.2)`

And the value of I when β = 72 dB is:

`\implies I=10^{\left((72)/(10)-12\right)}\\`

`\implies I=10^(-4.8)`

Percent Decrease formula

`\sf Percent\:decrease=(original\:value-new\:value)/(original\:value) * 100`

Therefore, the percent decrease is:

`\implies (10^(-3.2)-10^(-4.8))/(10^(-3.2)) * 100`

`\implies 97.4881135...\%`

`\implies 97.49\%\; \sf (2\; d.p.)`