Answer:
a) No inverse function
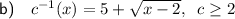
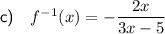
Explanation:
Part a
Given function:
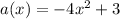
To find the inverse of the function, swap x and y:
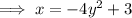
Rearrange the equation to isolate y:

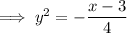
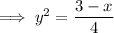
As the domain and range of function a(x) are unrestricted, the inverse relation is a “sideways” parabola and therefore it is not a function, since it fails the vertical line test.
Part b
Given function:

As the domain of function c(x) is restricted to x ≥ 5, the range is also restricted.
To find the inverse of the function, swap x and y:
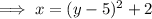
Rearrange the equation to isolate y:


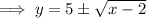
As the domain of function c(x) is restricted to x ≥ 5 then:
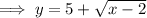
Replace y with c⁻¹(x):
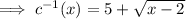
The domain of the inverse of a function is the same as the range of the original function. Therefore, the domain of the inverse function is restricted to x ≥ 2.
Part c
Given function:
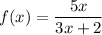
To find the inverse of the function, swap x and y:
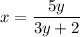
Rearrange the equation to isolate y:

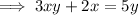

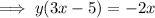
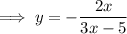
Replace y with f⁻¹(x):
