Question

NO LINKS!! NOT MULTIPLE CHOICE!!

For each of the functions below, find the following information. Then sketch a graph.
a. x- int and y-int.
b. vertical asymptote(s) or any holes
c. end behavior asymptotes
d. domain and range

33. g(x) = (x - 2)/(x^2 - 2x - 3)

34. k(x)= (x^2 - x - 2)/(x - 3)

35. f(x)= -x/(x^3 - 4x)

Answer 1

Question 33

a) x-int (2, 0). y-int (0, 2/3)

b) Vertical asymptotes: x = -1 and x = 3

Horizontal asymptote: y = 0

c) f(x) → -∞, as x → -1⁻

f(x) → +∞, as x → -1⁺

f(x) → -∞, as x → 3⁻

f(x) → +∞, as x → 3⁺

d) Domain: (-∞, -1) ∪ (-1, 3) ∪ (3, ∞)

Range: (-∞, ∞)

Question 34

a) x-int (-1, 0) and (2,0). y-int (0, 2/3)

b) Vertical asymptote: x = 3

c) f(x) → -∞, as x → 3⁻

f(x) → +∞, as x → 3⁺

d) Domain: (-∞, 3) ∪ (3, ∞)

Range: (-∞, 1] ∪ [9, ∞)

Question 35

a) No axis intercepts

b) Vertical asymptotes: x = -2 and x = 2. Hole at (0, ¹/₄).

c) f(x) → -∞, as x → -2⁻

f(x) → +∞, as x → -2⁺

f(x) → +∞, as x → 2⁻

f(x) → -∞, as x → 2⁺

d) Domain: (-∞, -2) ∪ (-2, 0) ∪ (0, 2) ∪ (2, ∞)

Range: (-∞, 0) ∪ (¹/₄, ∞)

Explanation:

Definitions

• The x-intercepts are the points at which the curve crosses the x-axis, so when y = 0.
• The y-intercept is the points at which the curve crosses the y-axis, so when x = 0.
• The domain of a function is the set of all possible input values (x-values).
• The range of a function is the set of all possible output values (y-values).
• A vertical asymptote occurs at the x-value(s) that make the denominator of a rational function zero.
• A horizontal asymptote occurs at y = 0 if the degree of the numerator is less than the degree of the denominator.
• A hole occurs when a rational function has a factor with an x that is in both the numerator and the denominator.

Question 33

Given rational function:

`g(x) =(x - 2)/(x^2 - 2x - 3)`

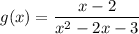
x-intercept

`\begin{aligned}y=0 \implies (x - 2)/(x^2 - 2x - 3)&=0\\x - 2&=0\\x&=2\end{aligned}`

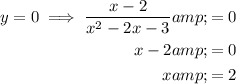
y-intercept

`x=0 \implies (0 - 2)/(0^2 - 2(0) - 3)=(2)/(3)`

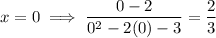
Vertical asymptotes

Set the denominator to zero and solve for x:

`\implies x^2-2x-3=0`

`\implies x^2-3x+x-3=0`

`\implies x(x-3)+1(x-3)=0`

`\implies (x+1)(x-3)=0`

`\implies x+1=0 \implies x=-1`

`\implies x-3=0 \implies x=3`

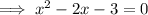
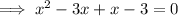
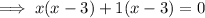
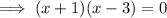
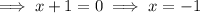
Horizontal asymptote

As the degree of the numerator is less than the degree of the denominator, there is a horizontal asymptote at y = 0.

Holes

Factor the denominator:

`g(x) =(x - 2)/((x+1)(x-3))`

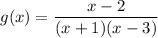
There are no holes as there is no common factor in the numerator and the denominator.

End behaviour near the vertical asymptotes

f(x) → -∞, as x → -1⁻

f(x) → +∞, as x → -1⁺

f(x) → -∞, as x → 3⁻

f(x) → +∞, as x → 3⁺

Domain

As there are vertical asymptotes at x = -1 and x = 3, the domain is restricted:

• Interval notation: (-∞, -1) ∪ (-1, 3) ∪ (3, ∞)

Range

The range is unrestricted:

• Interval notation: (-∞, ∞)

Question 34

Given rational function:

`k(x)= (x^2 - x - 2)/(x - 3)`

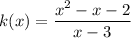
x-intercepts

`\begin{aligned}y=0 \implies (x^2 - x - 2)/(x - 3)&=0\\x^2 - x - 2&=0\\x^2-2x+x-2&=0\\x(x-2)+1(x-2)&=0\\(x+1)(x-2)&=0\\\\x+1&=0 \implies x=-1\\x-2&=0 \implies x=2\end{aligned}`

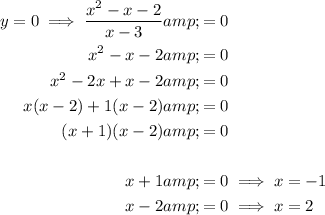
y-intercept

`x=0 \implies ((0)^2 - 0 - 2)/(0 - 3)=(2)/(3)`

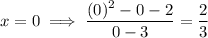
Vertical asymptotes

Set the denominator to zero and solve for x:

`\implies x-3=0`

`\implies x=3`

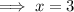
Holes

Factor the numerator:

`k(x)= ((x+1)(x-2))/(x - 3)`

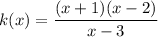
There are no holes as there is no common factor in the numerator and the denominator.

End behaviour near the vertical asymptote

f(x) → -∞, as x → 3⁻

f(x) → +∞, as x → 3⁺

Domain

As there is vertical asymptote at x = 3, the domain is rest:

• Interval notation: (-∞, 3) ∪ (3, ∞)

Range

The extreme points are (1, 1) and (5, 9). Therefore, the range is restricted:

• Interval notation: (-∞, 1] ∪ [9, ∞)

Question 35

Given rational function:

`f(x)= -(x)/(x^3 - 4x)`

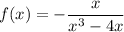
x-intercepts

As the degree of the numerator is less than the degree of the denominator, there is a horizontal asymptote at y = 0. Therefore, there are no x-intercepts.

y-intercept

Substitute x = 0 and solve for y:

`x=0 \implies -(0)/(0(x+2)(x-2))=(0)/(0)=\textsf{unde\:\!fined}`

Therefore, there is no y-intercept.

Factor the denominator:

`f(x)= -(x)/(x(x+2)(x-2))`

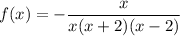
Cancel the common factor x:

`f(x)= -(1)/((x+2)(x-2))`

Vertical asymptotes

Set the denominator to zero and solve for x:

`\implies (x+2)(x-2)=0`

`\implies x+2=0 \implies x=-2`

`\implies x-2=0 \implies x=2`

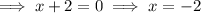
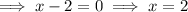
Holes

Factor the denominator:

`f(x)= -(x)/(x(x+2)(x-2))`

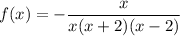
As the numerator and denominator have a common factor of x, the function is not defined when x = 0. Therefore, there is a hole when x = 0.

To find the y-value of the hole, cancel the common factor x and input x = 0 into the resulting function:

`x=0 \implies -(1)/((0+2)(0-2))=(1)/(4)`

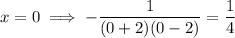
Therefore, there is a hole at (0, ¹/₄).

End behaviour near the vertical asymptotes

f(x) → -∞, as x → -2⁻

f(x) → +∞, as x → -2⁺

f(x) → +∞, as x → 2⁻

f(x) → -∞, as x → 2⁺

Domain

As there are vertical asymptotes at x = -2 and x = 2, and a hole at (0, ¹/₄), the domain is restricted:

• Interval notation: (-∞, -2) ∪ (-2, 0) ∪ (0, 2) ∪ (2, ∞)

Range

As there is a hole at (0, ¹/₄) and a horizontal asymptote at y = 0, the range is restricted:

• Interval notation: (-∞, 0) ∪ (¹/₄, ∞)