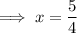Question

NO LINKS!!

Solve each equation. Be sure to check for extraneous solutions. Part 1

h. 20(1/2)^x/3 = 5
i. 2e^(2n-5) + 4 = 36
j. log₉x + 2log₉4= log₉20

Answer 1

`\textsf{h)} \quad x=6`

`\textsf{i)} \quad n = 2\ln 2+(5)/(2)`

`\textsf{j)} \quad x=(5)/(4)`

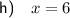
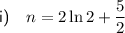
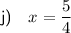
Explanation:

Part h

Given equation:

`20\left((1)/(2)\right)^{(x)/(3)} = 5`

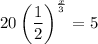
Divide both sides by 20:

`\implies\left((1)/(2)\right)^{(x)/(3)} = (20)/(5)`

`\implies\left((1)/(2)\right)^{(x)/(3)} =(1)/(4)`

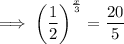
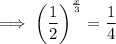
Rewrite 1/4 as (1/2)²:

`\implies\left((1)/(2)\right)^{(x)/(3)} =\left((1)/(2)\right)^2`

`\textsf{Apply exponent rule} \quad a^(f(x))=a^(g(x)) \implies f(x)=g(x)`

`\implies (x)/(3)=2`

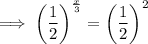
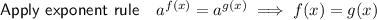
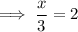
Multiply both sides by 6:

`\implies x=6`

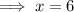
Part i

Given equation:

`2e^(2n-5) + 4= 36`

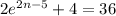
Subtract 4 from both sides:

`\implies 2e^(2n-5) = 32`

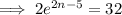
Divide both sides by 2:

`\implies e^(2n-5) = 16`

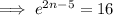
Take natural logs of both sides:

`\implies \ln e^(2n-5) = \ln 16`

`\textsf{Apply the power law}: \quad \ln x^n=n \ln x`

`\implies (2n-5)\ln e = \ln 16`

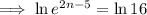
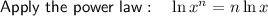
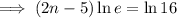
Apply the law ln(e) = 1:

`\implies 2n-5 = \ln 16`

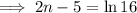
Rewrite 16 as 2⁴:

`\implies 2n-5 = \ln 2^4`

`\implies 2n-5 = 4\ln 2`

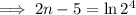
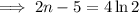
Add 5 to both sides:

`\implies 2n = 4\ln 2+5`

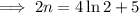
Divide both sides by 2:

`\implies n = 2\ln 2+(5)/(2)`

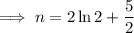
Part j

Given equation:

`\log_9x + 2\log_94= \log_920`

`\textsf{Apply the log power law}: \quad n\log_ax=\log_ax^n`

`\implies \log_9x + \log_94^2= \log_920`

`\implies \log_9x + \log_916= \log_920`

`\textsf{Apply the log product law}: \quad \log_ax + \log_ay=\log_axy`

`\implies \log_916x= \log_920`

`\textsf{Apply the log equality law}: \quad \textsf{If $\log_ax=\log_ay$ then $x=y$}`

`\implies 16x=20`

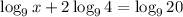
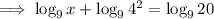
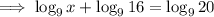
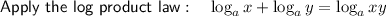
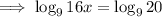
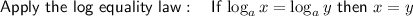
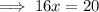
Divide both sides by 16:

`\implies x=(20)/(16)`

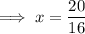
Simplify:

`\implies x=(5)/(4)`