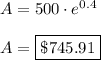Question

NO LINKS!!! NOT MULTIPLE CHOICE!!

59. You put $500 into a bank account that earns 2% interest. Determine each of the following.

a. The value of the account after 3 years if compounded annually.
b. The value of the account after 5 years if compounded quarterly.
c. The value of the account after 10 years if compounded monthly.
d. The value of the account after 20 years if compounded continously.

Answer 1

`a. \;\; \boxed{\$ 530.60}`

`b.\; \;\boxed{ \$552.45}`

`c,\;\;\boxed{\$610.60}`

`d. \;\; \boxed{\$745.91}`

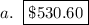
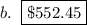
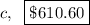
Explanation:

All four cases deal with compound interest on the same amount of $500 and same interest rate of 2%.

The only difference is in the frequency of compounding and time

Compound Interest Formula

`\boxed{A = P\left(1 + (r)/(n)\right)^(n\cdot t)\\\\}`

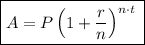
where

• P = amount initially deposited - principal amount

• A = accrued value which is principal amount + interest

• r = interest rate expressed as a decimal

• n = number of compounding intervals.
  This will depend on the frequency of compounding - daily, monthly, quarterly or yearly
  
• t = number of number of years under consideration
  

In this particular problem we have
P = $500
r = 2% = 0.02

These are common for all parts of the question
Only n an t are different for each of the question sub-parts

Part a

Compounding is done annually (once a year) for 3 years

n = 1
t = 3 years
n · t = 3

`A = 500\left(1 + (0.02)/(1)\right)^3\\\\A = 500\left(1.02\right)^3\\\\A = 500(1.061208)\\\\A=\boxed{\$ 530.60}`

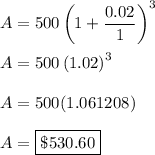
For accuracy of calculations, I will not compute and store the exponent part, I will perform the calculations in one shot

Part b

Here the compounding is done quarterly (4 times a year) for 5 years

n = 4
t = 5 years
nt = 4 · 5 = 20

`A = 500\left(1 + (0.02)/(4)\right)^(20)\\\\\\A = 500(1.005)^(20)\\\\A =\boxed{ \$552.45}`

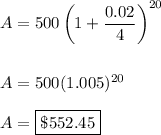
Part c

Compounding done monthly(12 times a year) for 10 years

n = 12

t = 10

nt = 120

`A = 500\left(1 + (0.02)/(12)\right)^(120)\\\\\\A = \boxed{\$610.60}`

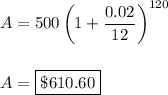
Part d

First let's figure out what continuous compounding means

The formula for continuous compounding can be determine by using the standard formula for periodic compounding and taking limits as

`n \rightarrow \infty`

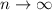
Therefore, for compounding continuously , the formula can be derived from

`\lim _(n\to \infty ) P\left(1 + (r)/(n)\right)^(nt)\\\\`

One of the limit formulas states

`\lim _(x\to \infty ) \left(1 + (a)/(x)\right)^(x) = e^a\\\\`

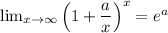
Therefore

`\lim _(n\to \infty ) \left(1 + (r)/(n)\right)^(n) = e^r\\\\`

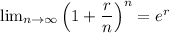
So for the continuous compounding case, the formula is

`\boxed{A = P \cdot e^(rt)}`

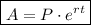
Here we have
r = 0.02
t = 20 years
rt = 20(0.02) = 0.4

Plugging in P = 500, and rt = 0.4 we get

`A = 500 \cdot e^(0.4)\\\\A = \boxed{\$745.91}`

Answer 2

a) $530.60

b) $552.45

c) $610.60

d) $745.91

Explanation:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Part a

Given:

• P = $500
• r = 2% = 0.02
• t = 3 years
• n = 1 (annually)

Substitute the given values into the compound interest formula and solve for A:

`\implies A=500\left(1+(0.02)/(1)\right)^(1 \cdot 3)`

`\implies A=500\left(1.02\right)^(3)`

`\implies A=500(1.061208)`

`\implies A=530.604`

Therefore, the value of the account after 3 years if interest is compounded annually is $530.60 (nearest cent).

Part b

Given:

• P = $500
• r = 2% = 0.02
• t = 5 years
• n = 4 (quarterly)

Substitute the given values into the compound interest formula and solve for A:

`\implies A=500\left(1+(0.02)/(4)\right)^(4 \cdot 5)`

`\implies A=500\left(1.005\right)^(20)`

`\implies A=500(1.10489557...)`

`\implies A=552.447788...`

Therefore, the value of the account after 5 years if interest is compounded quarterly is $552.45 (nearest cent).

Part c

Given:

• P = $500
• r = 2% = 0.02
• t = 10 years
• n = 12 (monthly)

Substitute the given values into the compound interest formula and solve for A:

`\implies A=500\left(1+(0.02)/(12)\right)^(12 \cdot 10)`

`\implies A=500\left(1.0016666...\right)^(120)`

`\implies A=500(1.22119943...)`

`\implies A=610.599716...`

Therefore, the value of the account after 10 years if interest is compounded monthly is $610.60 (nearest cent).

Part d

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

Given:

• P = $500
• r = 2% = 0.02
• t = 20 years

Substitute the given values into the continuous compounding interest formula and solve for A:

`\implies A=500e^(0.02 \cdot 20)`

`\implies A=500e^(0.4)`

`\implies A=500(1.49182469...)`

`\implies A=745.912348...`

Therefore, the value of the account after 20 years if interest is compounded continuously is $745.91 (nearest cent).