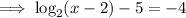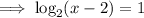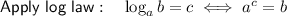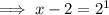Question

NO LINKS!!
Consider the function f(x) = log₂(x - 2) - 5

Answer 1

a) See attachment.

b) Domain: (2, ∞)

Range: (-∞, ∞)

c) As x → 2⁺, f(x) → -∞

As x → ∞, f(x) → ∞

d) f(3) = -5

e) x = 4

Explanation:

Given logarithmic function:

`f(x)=\log_2(x-2)-5`

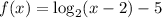
Part a

As the argument of a log function can only take positive arguments, the domain is restricted to x > 2 and there is a vertical asymptote at x = 2.

To find the x-intercept, set the function to zero and solve for x:

`\implies \log_2(x-2)-5=0`

`\implies \log_2(x-2)=5`

`\textsf{Apply log law}: \quad \log_ab=c \iff a^c=b`

`\implies x-2=2^5`

`\implies x-2=32`

`\implies x=34`

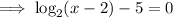
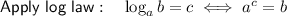
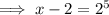
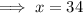
Therefore, the x-intercept is (34, 0).

Substitute x = 10 into the function to find a second point on the curve:

`\implies f(10)=\log_2(10-2)-5`

`\implies f(10)=\log_2(8)-5`

`\implies f(10)=\log_2(2)^3-5`

`\implies f(10)=3\log_2(2)-5`

`\implies f(10)=3(1)-5`

`\implies f(10)=3-5`

`\implies f(10)=-2`

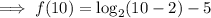
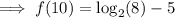
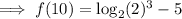
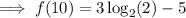
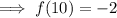
Therefore, a second point on the curve is (10, -2).

Part b

As the argument of a log function can only take positive arguments, the domain is restricted to x > 2:

• Interval notation: (2, ∞)

The range is unrestricted:

• Interval notation: (-∞, ∞)

Part c

As x approaches x = 2 from the positive side, the function approaches negative infinity:

• As x → 2⁺, f(x) → -∞

As x approaches positive infinity, the function approaches positive infinity.

• As x → ∞, f(x) → ∞

Part d

From inspection of the graph:

• f(3) = -5

Check by evaluating f(3) algebraically:

`\implies f(3)=\log_2(3-2)-5`

`\implies f(3)=\log_2(1)-5`

`\implies f(3)=0-5`

`\implies f(3)=-5`

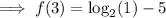
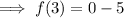
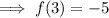
Part e

From inspection of the graph:

• f(x) = -4 ⇒ x = 4

Check by evaluating f(x) = -4 algebraically:

`\implies \log_2(x-2)-5=-4`

`\implies \log_2(x-2)=1`

`\textsf{Apply log law}: \quad \log_ab=c \iff a^c=b`

`\implies x-2=2^1`

`\implies x-2=2`

`\implies x=4`