Answer:
v=-5 and v=3
Explanation:
We are given that
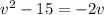
We have to find two solutions of quadratic equation.
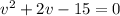
Using addition property of equality
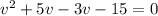 (By using factorization method)
(By using factorization method)
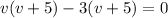
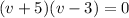
Substitute each factor equal to 0
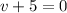 and
and
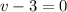
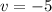 and
and
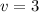
Hence, two solutions of quadratic equation are
v=-5 and v=3