Question

So confused
DUE SOON PLEASE HELP IM SO CONFUSED ​

Answer 1

1) Mean = $75812.50

Median = $74000

Mode = $73100

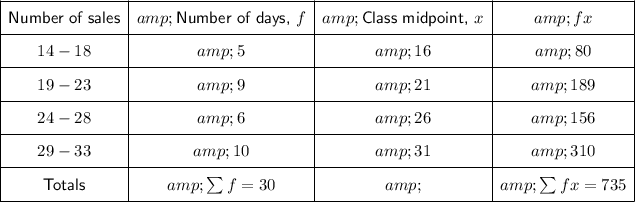
2) Mean = 24.5

Median = 24.33333...

Modal class = 29 - 33

Explanation:

Definitions

• The mode is the most frequently occurring data value.
• The median is the middle value when all data values are placed in order of size.
• The mean is the sum of all data values divided by the total number of data values.

Question 1

Given data:

• 71500, 74900, 69700, 82300, 78500, 73100, 73100, 83400

Mean

`\begin{aligned}\textsf{Mean}&=(71500+74900+69700+82300+78500+73100+73100+83400)/(8)\\ &= (606500)/(8)\\&=75812.50\end{aligned}`

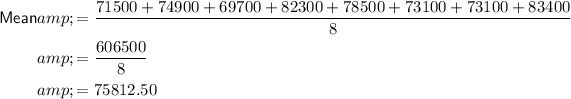
Median

Place the data values in order of size (smallest to largest):

• 69700, 71500, 73100, 73100, 74900, 78500, 82300, 83400

As there is an even number of data values, the median is the mean of the middle two values:

`\implies \sf Median=(73100+74900)/(2)=74000`

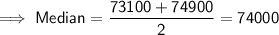
Mode

The most frequently occurring data value is $73100. Therefore:

`\implies \textsf{Mode} = 73100`

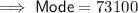
Question 2

With grouped data, we can only estimate the mean and median.

Mean

To find an estimate of the mean, assume that every reading in a class takes the value of the class midpoint.

The number of days is the frequency (f).

Add a class midpoint (x) and an fx column to the table:

`\begin{array}c\cline{1-4}\vphantom{\frac12} \sf Number\;of\;sales&\textsf{Number of days, $f$}&\textsf{Class midpoint, $x$}&fx\\\cline{1-4}\vphantom{\frac12}14-18&5&16&80\\\cline{1-4}\vphantom{\frac12}19-23&9&21&189\\\cline{1-4}\vphantom{\frac12}24-28&6&26&156\\\cline{1-4}\vphantom{\frac12}29-33&10&31&310\\\cline{1-4}\vphantom{\frac12}\sf Totals&\sum f=30&&\sum fx=735\\\cline{1-4}\end{array}`

`\textsf{Mean}=(\sum fx)/(\sum f)=(735)/(30)=24.5`

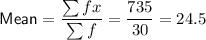
Median

To find an estimate for the median, use linear interpolation.

Add a cumulative frequency column to the table:

`\begin{array}c\cline{1-3}\vphantom{\frac12} \sf Number\;of\;sales&\textsf{Number of days}&\textsf{Culmulative frequency}\\\cline{1-3}\vphantom{\frac12}14-18&5&5\\\cline{1-3}\vphantom{\frac12}19-23&9&14\\\cline{1-3}\vphantom{\frac12}24-28&6&20\\\cline{1-3}\vphantom{\frac12}29-33&10&30\\\cline{1-3}\end{array}`

Find which class the median is in.

Since n/2 = 30/2 = 15, there are 15 values less than or equal to the median. This means the median must be in the 24-28 class.

Therefore:

• 
  `a_1=m-23.5`
• 
  `b_1=28.5-23.5=5`
• 
  `a_2=15-14=1`
• 
  `b_2=20-14=6`

To find the median, m:

`\begin{aligned}(a_1)/(b_1)=(a_2)/(b_2) \implies (m-23.5)/(5)&=(1)/(6)\\\\ 6(m-23.5)&=5\\\\6m-141&=5\\\\6m&=146\\\\m&=24.3333...\end{aligned}`

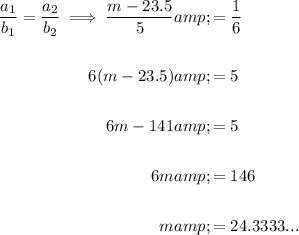
Therefore, the median is 24.3333...

Mode

The modal class is the class with the highest frequency density.

As all the classes are the same width, this is the class with the highest frequency.

• Modal class = 29 - 33