Question

Find derivative
f'(x) =​

Answer 1

`\displaystyle{f'(x)=(9)/(4)x\left(8x^4+x^2-1\right)^{(1)/(8)}(16x^2+1)}`

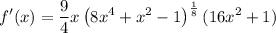
Explanation:

Given the function
`\displaystyle{f(x)=\sqrt[8]{\left(8x^4+x^2-1\right)^9}}`. We can rewrite the function in exponential form as
`\displaystyle{f(x)=\left(8x^4+x^2-1\right)^{(9)/(8)}}`. Here, we have to know the power rules and the chain rule:

`\displaystyle{f(x) = u^n \to f'(x) = nu^(n-1) \cdot (du)/(dx)}`

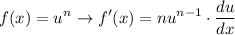
Therefore, from the above formula, we will have:

`\displaystyle{f'(x)=(9)/(8)\left(8x^4+x^2-1\right)^{(9)/(8)-1} \cdot (d)/(dx)\left(8x^4+x^2-1\right)}\\\\\displaystyle{f'(x)=(9)/(8)\left(8x^4+x^2-1\right)^{(9)/(8)-(8)/(8)} \cdot (d)/(dx)\left(8x^4+x^2-1\right)}\\\\\displaystyle{f'(x)=(9)/(8)\left(8x^4+x^2-1\right)^{(1)/(8)} \cdot (d)/(dx)\left(8x^4+x^2-1\right)}`

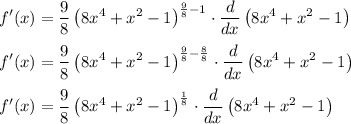
Next, we derive the function 8x⁴ + x² - 1 by applying the power rules:

`\displaystyle{f(x) = x^n \to f'(x) = nx^(n-1) \cdot (dx)/(dx) \to f'(x)=nx^(n-1)}`

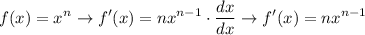
Also, deriving any constants will result in 0 always.

Therefore:

`\displaystyle{(d)/(dx)\left(8x^4+x^2-1\right)} = 4\cdot 8 x^(4-1) + 2\cdot x^(2-1) - 0}\\\\\displaystyle{(d)/(dx)\left(8x^4+x^2-1\right)} = 32x^3 + 2x}`

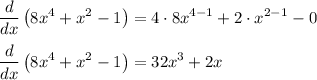
Thus, we will have:

`\displaystyle{f'(x)=(9)/(8)\left(8x^4+x^2-1\right)^{(1)/(8)} \cdot (32x^3+2x)}\\\\\displaystyle{f'(x)=(9)/(8)\left(8x^4+x^2-1\right)^{(1)/(8)} \cdot 2x(16x^2+1)}\\\\\displaystyle{f'(x)=(9)/(4)x\left(8x^4+x^2-1\right)^{(1)/(8)}(16x^2+1)}`

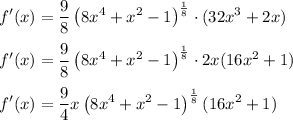
Therefore, the derivative is:

`\displaystyle{f'(x)=(9)/(4)x\left(8x^4+x^2-1\right)^{(1)/(8)}(16x^2+1)}`

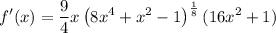
or you can rewrite in the form of surd as:

`\displaystyle{f'(x)=(9)/(4)x(16x^2+1)\sqrt[8]{8x^4+x^2-1}}`