Question

Carla’s dining room and living room have the same perimeter. The width of her rectangular dining room is 18 feet, and the width of her rectangular living room is 12 feet. The length of her dining room is 1 foot less than 3/4 the length of her living room. What is the length of Carla’s living room?

Answer 1

Length of Carla's living room is 20 feet

Explanation:

The perimeter of a rectangle is 2(L + W)
In the case of both dining and living rooms, we are given the widths as dining room width = 18, living room width = 12 and asked to calculate living room length from the information given

Let x be the length of the dining room and y the length of the living room

Perimeter of dining room = 2(18 + x)

Perimeter of living room = 2(12 + y)

Since these are equal
2(18 + x) = 2(12 + y)

=> 18 + x = 12 + y

Subtract x from both sides:
18 = 12 + y - x

Subtract 12 from both sides:
18 - 12 = y - x

Simplifying and rearranging terms we get

- x + y = 6 [1]

We are also given that:
The length of her dining room is 1 foot less than 3/4 the length of her living room.

This mathematically translates to:

`x = (3)/(4)y - 1`

which can be re-written as

`x - (3)/(4) = -1 \; \cdots[2]`

So the two equations are

`- x + y = 6 \;\cdots [1]`

`x - (3)/(4)y = - 1 \; \cdots [2]`

Notice that the coefficients of x are the same(1) but with opposite signs

Add [1] and [2]

`(-x + y) +(x - (3)/(4)y) = 6 - 1\\\\-x + x + y - (3)/(4)y = 5\\\\(1)/(4)y = 5\\\\y = 20\\\\`

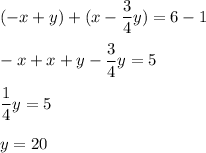
So the length of the living room is 20 feet

(If you wanted to find the length of the dining room, substitute 20 into equation 1 to get -x + 20 = 6 which will give x = 14 and is the length of the dining room)