Question

The value of y is ____ units. Round answer to tenths.

Answer 1

y = 5.2

Explanation:

We can use the laws of sine to solve for this, the laws of sine state that:

`\displaystyle{(\sin A)/(a)=(\sin B)/(b) = (\sin C)/(c) = 2R}`

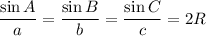
In this diagram, we can rewrite the general form of sinA, sinB, sinC as:

`\displaystyle{(\sin F)/(f)=(\sin E)/(e) = (\sin D)/(d) = 2R}`

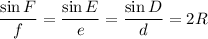
We can use the equation of
`\diplaystyle{(\sin F)/(f) = (\sin E)/(e)}` to solve for the value of e. In this case, f is 7 since sides are opposite to measurements, and the opposite of measurement F is side length 7 units. The opposite side of measurement E is side length y units. Hence, f = 7 and e = y.

`\diplaystyle{(\sin F)/(7) = (\sin E)/(y)}`

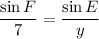
We know that the measurement E is 48°.

`\diplaystyle{(\sin F)/(7) = (\sin 48 \textdegree)/(y)}`

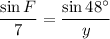
We can find the measurement F by using the euclidean triangle theory that all sides will add up to 180°. This will result in 42° + 48° + F = 180. Solve the equation:

`\displaystyle{90 \textdegree + F = 180 \textdegree}\\\\\displaystyle{F = 180 \textdegree - 90 \textdegree}\\\\\displaystyle{F = 90 \textdegree}`

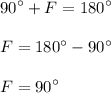
Hence, the measurement of F will equal to 90°.

`\diplaystyle{(\sin 90 \textdegree)/(7) = (\sin 48 \textdegree)/(y)}`

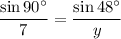
Solve the equation for y by firstly multiplying both sides by 7y to clear off denominators.

`\diplaystyle{(\sin F)/(7) \cdot 7y = (\sin 48 \textdegree)/(y) \cdot 7y}\\\\\displaystyle{y\sin 90 \textdegree = 7\sin 48 \textdegree}`

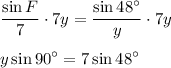
We know that sin90° = 1 so we will have
`\displaystyle{y=7\sin 48 \textdegree}`. Now input the value in a calculator since we cannot evaluate sin48° with an ordinary method.

When you put 7sin48° in a calculator, you will get 5.20201377... then you round the value to nearest tenth. Hence, y is 5.2 units.