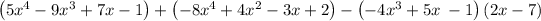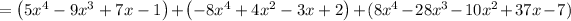Question

Simplify the following polynomial expression.

(5x^4 - 9x^3 + 7x -1) + (-8^4 - 3x + 2) - (-4x^3 + 5x - 1) (2x - 7)

Answer 1

`\boxed{\mathrm{Option \;D: 5x^4-37x^3-6x^2+41x-6}}`

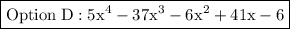
Explanation:

You can solve such multiple choice questions using a trick. This especially is useful in a time constrained question

Consider only the coefficients of the terms relating to x⁴ and the constant

If you expand (-4x³ + 5x - 1)(2x - 7) this will work out to

(--4x³) (2x) +..... + (-1)(-7)

This will result in (- 8x⁴ +..... + 7)

Since there is a negative sign before this last term, expanding will change the signs of the terms

-(-8x⁴ + ..... + 7) = 8x⁴ -7

Add the coefficients of the x⁴ terms to get

(5 - 8 + 8)x⁴ = 5x⁴

Add the constants of the individual terms

--1 + 2 - 7 which is -6

So the simplified polynomial is of the form

5x⁴ +....... - 6

Only option D fits these values, so the correct choice is Option D:

`\mathrm{5x^4-37x^3-6x^2+41x-6}`

ANSWER

--------------------------------------------------------------------------------------------------

If you want to do it the hard way,

First evaluate the last product using FOIL:

`\left(-4x^3+5x-1\right)\left(2x-7\right)\\\\= \left(-4x^3\cdot \:2x-4x^3\left(-7\right)+5x\cdot \:2x+5x\left(-7\right)-1\cdot \:2x-1\cdot \left(-7\right)\right)\\\\= \left(-8x^4+28x^3+10x^2-37x+7\right)\\\\`

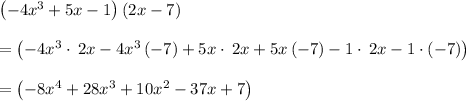
With the negative sign in front of this expression this becomes:

`-\left(-8x^4+28x^3+10x^2-37x+7\right)\\\\= 8x^4-28x^3-10x^2+37x-7\\\\`

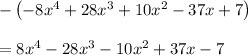
From the original polynomial expression, group like terms:

`\left(5x^4-9x^3+7x-1\right)+\left(-8x^4+4x^2-3x+2\right)-\left(-4x^3+5x\:-1\right)\left(2x-7\right)\\\\`

`=\left(5x^4-9x^3+7x-1\right)+\left(-8x^4+4x^2-3x+2\right) + (8x^4-28x^3-10x^2+37x-7)\\\\`