Question

the length of a rectangular platform is 2 feet longer than three times its width. The area of the platform is 56 square feet. Write a polynomial that represents the area of the platform

Answer 1

The area of the platform :

56 = (3x+2) × x

Explanation (+ solving for x)

Let the width of Rectangular Platform is x feet.

Then,

Length of Rectangular Platform is (3x+2) feet

Area of Rectangular Platform = Length × width

`56=(3x+2) × x \\ 56 = 3x² + 2x \\ 3x² +2x-56= 0 \\ x = \frac{ -2±\sqrt{ {2}^(2) - 4 * 3 * ( - 56)} }{2 * 3} \\ = (-2± √(4 + 672) )/(6) \\ = ( - 2±26)/(6) \\ = - (28)/(6) or \: 4`

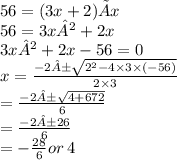
Since x can't be negative,

Value of x is 4 feet.

So, width of Platform= 4

feet Length of Platform = 14 feet