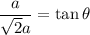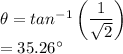Question

Find the angle between a diagonal of a cube and one of its faces ?

Answer 1

35.26°

Explanation:

You have to visualize this or draw a diagram

If a cube has side a, the face diagonal of the cube is √2a . The diagonal of the cube is √3a

One side of length a, another side of length √2a (face diagonal) and the third of √3a form a right triangle with the angle opposite √3a being the 90° angle

Therefore we can find the angle
`\theta` which the cube diagonal makes with the face diagonal using the fact

`(a)/(√(2)a) = \tan\theta`

`\theta = tan^(-1)\left((1)/(√(2)\right)) \\= 35.26^\circ`