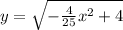Question

What is the result of isolating y^2 in the equation below? 4x^2 + 25y^2= 100

Answer 1

In factored form:
`y=\sqrt{-(1)/(25)(2x-10)(2x+10)}`

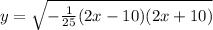
In standard form:
`y=\sqrt{-(4)/(25)x^2+4}`

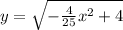
Explanation:

Generally for these type of equations we want to get the term with "y" by it self (ignoring coefficients and any operations such as square root, etc...) so we want to get rid of the
`4x^2` from the left side which we can do by subtracting this from both sides to maintain equality and get rid of it on the left side.

`25y^2=-4x^2+100`

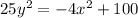
One thing I want to note here is we can actually factor the right side which we generally want to do, we can rewrite it as:
`-(4x^2-100)` and from here we have a difference of squares:
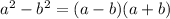`a^2-b^2=(a-b)(a+b)` so we can rewrite this as:
`-(2x-10)(2x+10)`

`25y^2=-(2x-10)(2x+10)`

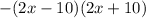
From here we divide both sides by 25:

`y^2=-(1)/(25)(2x-10)(2x+10)`

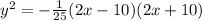
Now from here to get rid of that square we do the inverse which is taking the square root:

`y=\sqrt{-(1)/(25)(2x-10)(2x+10)}`

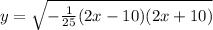
The reason factoring is useful in this case is we can now easily determine the domain of the function since inside the square root we have a quadratic which is opening down meaning it's only not negative between the zeroes (including the zeroes since they're... zero not negative) and this would be the domain of the graph. But if we wanted it to not be in factored form we would just put back what we had so we would have:

`y=\sqrt{-(1)/(25)(4x^2-100)}`

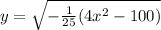
then distribute the -1/25 to get:

`y=\sqrt{-(4)/(25)x^2+4}`