Question

From the observation deck of a skyscraper, Morgan measures a 67∘ angle of depression to a ship in the harbor below. If the observation deck is 955 feet high, what is the horizontal distance from the base of the skyscraper out to the ship? Round your answer to the nearest hundredth of a foot if necessary.

Answer 1

405.37

Explanation:

tan(67) = 955/ X

(tan(67) )(X), (955) (X)

X tan(67) = 955

X tan(67)/ tan(67) = 955/ tan(67)

X= 405.37

Answer 2

Answer: 405.37 feet

Explanation:

First, we need to draw a diagram of the situation. See attached of the picture I created.

Next, we will use trigonometric functions to solve for x. Of the given angle, we are given the adjacent side and are solving for the opposite side. We will use the tangent funcion.

tanθ =
`(opposite)/(adjcent)`

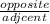
tan67 =
`(955)/(x)`

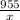
xtan67 = 955

x = 955/tan67

x = 955/2.35585

405.37 feet = x