Answer:
The equation of the tangent line passing through the point (-2,3) is
4 x + y +5 =0
Explanation:
Step(i):-
Given that the slope of the tangent
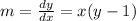
m = -2( 3-1) = -4
Given point x = -2
y = f(-2) =3
∴The given point ( x₁ , y₁) = ( -2 ,3)
Step(ii):-
The equation of the tangent line passing through the point (-2,3)
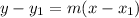
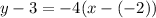
y -3 = -4( x+2)
y-3 = -4x -8
4x + y -3+8=0
4x +y +5=0
Step(iii):-
The equation of the tangent line passing through the point (-2,3) is
4 x + y +5 =0