Question

If dy/dx = x(y-1), find the equation of the tangent line at x=-2 with f(-2)=3

Answer 1

The equation of the tangent line passing through the point (-2,3) is

4 x + y +5 =0

Explanation:

Step(i):-

Given that the slope of the tangent

`m = (dy)/(dx) = x(y-1)`

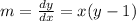
m = -2( 3-1) = -4

Given point x = -2

y = f(-2) =3

∴The given point ( x₁ , y₁) = ( -2 ,3)

Step(ii):-

The equation of the tangent line passing through the point (-2,3)

`y - y_(1) = m(x-x_(1) )`

`y -3 = -4(x-(-2))`

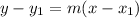
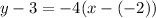
y -3 = -4( x+2)

y-3 = -4x -8

4x + y -3+8=0

4x +y +5=0

Step(iii):-

The equation of the tangent line passing through the point (-2,3) is

4 x + y +5 =0