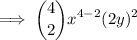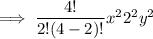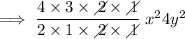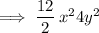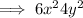Answer:
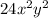
Explanation:

We can use the Binomial Theorem to find any term of a binomial expansion.
The first term is when k = 0, so the third term is when k = 2.
Compare the given expression (x + 2y)⁴ with the formula to find the values of a, b and n.
Therefore:
Substitute the values into the formula to find the third term: