Question

Any help please? I’m stuck at this question.

Answer 1

8/5 = 1 3/5

Explanation:

You want the value of the continued fraction shown.

Fraction

The fraction can be evaluated from the bottom up:

`1+\cfrac{1}{1+\cfrac{1}{1+(1)/(2)}}=1+\cfrac{1}{1+\cfrac{1}{\left((3)/(2)\right)}}=1+\cfrac{1}{1+\cfrac{2}{3}}=1+\cfrac{1}{\left(\cfrac{5}{3}\right)}\\\\\\=1+(3)/(5)=\boxed{(8)/(5)}`

__

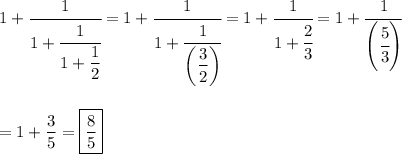
Additional comment

The left side of each sum as we go down the fraction can be listed as ...

a = {1, 1, 1, 2}

When the fraction numerator is 1 at every level, these values can be used in a recursive relation to develop the fraction value from the top down.

Let N(-1) = 0, N(0) = 1, D(-1) = 1, D(0) = 0. For value a(k), the next approximation to the fraction will be N(k)/D(k) where ...

• N(k) = a(k)·N(k-1) +N(k-2)
• D(k) = a(k)·D(k-1) +D(k-2)

Using the above list for a(k), the sequence of fractions starting from k=-1 is ...

0/1, 1/0, 1/1, 2/1, 3/2, 8/5

If this fraction had 1 + 1/( ) at every level, continuing indefinitely, its value would approach Φ = (1+√5)/2 ≈ 1.6180339887....

<95141404393>