Answer:
$807.39
Explanation:

Given:
- P = $500
- r = 4% = 0.04
- n = 12 (monthly)
- t = 12 years
Substitute the given values into the compound interest formula and solve for A:
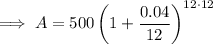
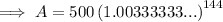
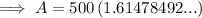
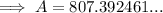
Therefore, Alyson will have $807.39 (nearest cent) in her account at the end of 12 years.