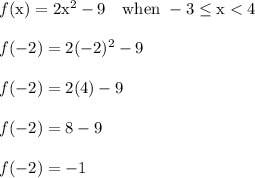Answer: -1
==========================================================
Step-by-step explanation:
This is the given piecewise function
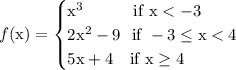
This is another way to look at the piecewise function
- If
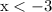 , then
, then
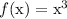
- If
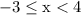 , then
, then

- If
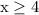 , then
, then
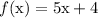
We have 3 different branches or pathways to take based on what the x input is.
We want to compute f(-2). This means we want to find f(x) when x = -2 is the input.
This input matches with the interval
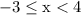 since
since
 is a true statement. Therefore, we'll use the second option
is a true statement. Therefore, we'll use the second option
-----------
Plug x = -2 into the second part to get...