Question

An object has 9000 J of kinetic energy and a mass of 35 kg. What is the object's speed ?

Answer 1

Answer:Therefore, the speed of the object that has 9000 J of kinetic energy and a mass of 35 kg is 22.68 m/s.

Step-by-step explanation:

An object has 9000 J of kinetic energy and a mass of 35 kg. What is the object's speed?

Data:

Ec = kinetic energy = 9000 J

m = mass = 35 kg

V = speed = ?

The formula of potential energy;

Ec = m * v²/2

Where

• Ec = kinetic energy
• m = mass
• V = speed

We clear for speed, substitute data and solve:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{Ec=(m*v^2)/(2) \iff \ V=\sqrt{(2*E_c)/(m) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{(2*9000 \ J)/(35 \ kg) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{(18000 \ J)/(35 \ kg) } } \end{gathered}$}}`

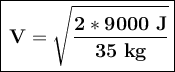
Before continuing to answer, we work with the units, which in this case is Joules.

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{(18000 \ N*m)/(35 \ kg) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{\frac{18000 \ \\ot{kg}*(m)/(s^2) *m}{35 \\ot{kg}} } \iff V=\sqrt{(1800 \ (m)/(s^2) *m)/(35) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{(18000 \ (m^2)/(s^2) )/(35 \ ) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{514.2857142857142857 \ (m^2)/(s^2) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=\sqrt{514.286 \ (m^2)/(s^2) } } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V=22.6778746799606422=22.6778 \ m/s } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V \approx22.68 \ m/s } \end{gathered}$}}`

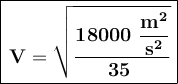
Therefore, the speed of the object that has 9000 J of kinetic energy and a mass of 35 kg is 22.68 m/s.