Answer: -3/2
Explanation:
To find the slope of the line perpendicular to the given one, we first need to change the equation to y=mx+b to find the original slope.
 [subtract both sides by -6x]
[subtract both sides by -6x]
 [divide both sides by -9]
[divide both sides by -9]
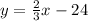
Now we know slope is 2/3. The slope of the perpendicular line is the opposite sign and reciprocal of the slope.
Opposite would make it -2/3.
Reciprocal would be -3/2.
So the slope is -3/2.